Can we use the rounding strategy to check answers for all four number operations (add, subtract, multiply, divide)?
We began by discussing our initial theories to this questions with our table partners to help start tuning in to the sort of thinking we will be doing.
Next, we had 5-10 minutes to investigate addition.
° Could we always use rounding to check if our addition sums were correct or not?
° Are there some numbers where the rounding strategy doesn't work? If so, why?
° Can we challenge our thinking by exploring this with decimal numbers?
After we had time to investigate, we published our findings / discoveries and some children shared with the class discoveries they had made. Some really interesting theories started to emerge with kids wondering:
° Do odd or even numbers makes a difference?
° If the difference in changing the numbers is greater than 5, the strategy doesn't work, but if the changed numbers totals less than 5, it does work. Is this really true? (see below)
We talked about how proving a theory we are testing is just as successful as disproving a theory. Some of us wondered if this is what professional mathematicians do?
We then repeated our rounding investigation with subtraction.
A few students came up with an amazing theory and excitedly tested it out.
They discovered that if you can round numbers successfully with addition, then those same numbers cannot round successfully with subtraction. Why not?
They tried to find this out and theorised that it might be because addition and subtraction are opposites. Such a great idea!
They were encouraged to further test numbers to test their new theory.
One student with a really strong number sense decided to investigate whether we can round numbers to check answers with positive and negative numbers. He discovered it does work with most negative numbers and shared his theory with us:
This is one of the great advantages to enquiry-based maths. Those children who need extending have the opportunity to take their thinking to deeper places that typical teacher-directed maths activity simple can't do. Equally children in the class with not-so-strong number senses could also explore numbers that they were comfortable with investigating.
We repeated our investigations with multiplication and finally with division.
Some children started expanding upon each other's theories to test and help deepen them which was amazing to observe. The same students who had come up with the 'if it works for addition, those same numbers won't work for subtraction' theory were excited to see if this also applied to multiplication and division. When they were testing this out, another student noted that perhaps it doesn't work with numbers that can be square-rooted. When they tested that theory out, they started to discover it does actually make a difference!
Kids sharing discoveries and theories they created and are testing out:
Some students wondered if it made a difference if we rounded the number we were dividing by or not?
These students shared their theory that if the number was below 5, we couldn't check using the rounding strategy, but if it was above 5, it would work!
This got others investigating if this would work with larger numbers....some wanted to see if it also worked with decimal numbers too!
All of these great theories to test out were student generated. They were arousing wonderful curiosity with each other and building upon their own theories. Quite the buzz of mathematical thinking!
Kids sharing their discoveries:
A sample of published discoveries:
Another student sample:
Another sample:
It was one of those great activities where kids could take their learning to such different aspects based upon their number sense and they all felt really proud of what they had discovered.
Are all their theories accurate? Maybe, maybe not.
I don't think that is so important for them to know. What IS important is that they gained a real sense of enquiring into numbers and feeling successful at it. They were beaming with pride with theories they were formulating and completely engaged in trying to prove or disprove them. That was the key essence of the learning experience. They gained a real sense of what mathematicians do and regardless of their maths number abilities, they all felt like really successful mathematicians - because they were!
Highlighting who was 'right' and who was 'wrong' with their discoveries would have been a counter-productive thing to do. What we want, is to inspire children to create their own deep thoughts about how numbers relate to each other, formulate their own theories and test them out. The 'right / wrong' approach would have killed that enthusiasm and curiosity that was flooding our room today.
Maths learning is too often drilled into children as a 'right / wrong' learning area.
It's not.
Maths is a science and should be presented as such. Just like scientists, mathematicians formulate theories and test them out. We need to give kids these sort of opportunities to allow them to discover how maths can be interesting and enjoyable and dare I say......actually rewarding!

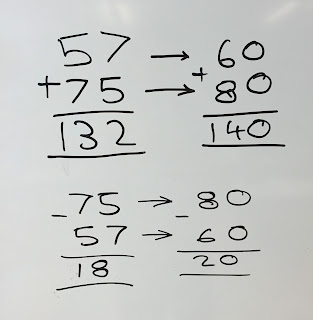










No comments:
Post a Comment
What do you think? ...........