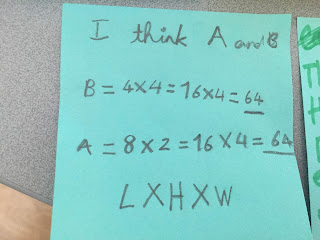Morning Prompt: What volume of water should we consume per day?

As we are exploring volume, our morning prompt for when the children entered our room at the beginning of the day whilst organising themselves to get ready was four beakers with different volumes of water.

Here is the invitation to the prompt:

And here is what the volumes looked like.

The first had 250mL, the second had 500mL, the third had 750mL and the fourth 1 . 5 litres.

It was really interesting to observe and listen into the reasoning discussions they were having amongst each other.

Some children drew upon prior knowledge about how much water adults need to consume and so they adjusted that amount to what they thought a child might require.

Some tried to estimate how much they personally would drink in a day and tried to match that estimate with a volume.

A few children began discussing whether they had to actually drink that volume or could the water also be included in the food they eat. 

Some others used reasoning skills to try to determine whether it would be 750 mL or 1. 5 litres. They had already eliminated the two smaller volumes as they felt they drank that much before lunch time. Their gut instinct was telling them that the 1 . 5 litres looked like A LOT of water, so perhaps it was more reasonable to think the 750 mL would be the amount.

One student had remembered reading that adults need to drink 8 cups per day, so he found a cup at our sink and brought it over beside the litre beaker to estimate how many cups that would equate to. He later decided to return to the sink and poured 8 cups of water into another litre jug to test his hypothesis.

Some of our thoughts:

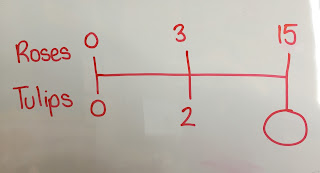
I liked this strategy of comparing his water bottle to the volumes of water shown:

Sharing prior knowledge about water being found in food:

Testing his own hypothesis based on prior knowledge:

There was a lot of genuine engagement and sharing of theories with this prompt. 

Later in the day, we discussed what we already knew about why we need to constantly drink water throughout the day.

In our class, we have a volunteer who is our 'Rehydrator of the Week'. Throughout the day, this person will raise their water bottle and shout out 'Cheers!' to the class.  When we hear that, we all raise our water bottles and say 'Cheers!' and then thank the rehydrator for reminding us to have a drink.

This is a fun routine we have, but it also (hopefully) is helping to create a habit for the children to be conscious of drinking water regularly. 

Over the year, we have discussed often the impacts of drinking water often to help our brains think to their best ability etc.

We also have a class 'energiser'. This person's responsibility is if they feel we have been sitting down for too long, they invite us to the front of the room and will demonstrate three body movements which we copy. The purpose of this is to help circulate the blood in our bodies which e understand carries oxygen to our brains that helps us to think more effectively. I'm hoping this routine will help create positive habits of staying alert and healthy.

We then watched this TedTalk about the benefits of drinking water and discussed some of the information it shared and our wonderings that emerged from it.

We then looked at our water volume prompt and shared some of the strategies we used to determine how much water we should drink.  Some of us were pretty shocked to see it was approximately 1 . 5 litres because it does, indeed look a lot!

In our discussion, some children shared some personal action plans to try to ensure they do drink more water throughout the day which was great to hear (even without our class rehydrator reminding us)

Another suggested we find a way to measure how much water we consume per day to see if we ae being healthy or not and so next week, we will use that idea and try to create a way to record this. This is a great example of giving children opportunities to take action with their learning. It will be interesting to see how our class decides to go about this.

I think these morning prompt routines are a really effective way to engage children in mathematical thinking. They are not mandatory to participate in which I think makes them work better. The children who choose to participate are genuinely engaged and that engagement (I suspect) creates more interest in those other children who might normally pass on the maths thinking opportunity. 

Measuring Volume Morning Prompt

For our morning walk in prompt when the children first enter our room and get organsied for the day, I set up two shapes that had the same volume.

With our morning prompts, children do not have to participate, but nearly all of them do at their own choice.

The question posed was which had a greater volume.

I wanted to give the children an opportunity to solidify their newly discovered strategy of measuring the volume of rectangular prisms. We hadn't looked at this for a few weeks so I was curious to see who would remember the formula and / or what other strategies would emerge.

Most of the children who participated could recognise that the two shapes had the same volume.  Most used the formula, but others chose other strategies. This become a useful informal assessment to see what each child was doing mathematically.


Some samples:

Later in the day, we revisited the prompt and discussed strategies we used. This was a helpful way for children to hear how others approach mathematical thinking.

It also ended up creating an interesting investigation which we decided to add to our wonder wall:   What other prisms can we create that have an equal volume?

I think some very interesting number connections could be explored with that and so I'm excited to see who will choose to explore it and what they discover.

Estimating Volume Morning Prompt

Providing children with invitations in the morning when the first enter the classroom can be an engaging way to appreciate mathematical thinking in different contexts.

As we are currently exploring measuring volume and capacity, I found a small jar of sweets and when the children entered, they could choose to try to estimate how many sweets were in the jar.

On their sticky note, they were asked to explain the strategy they used to estimate.

Later in the day when we visited the maths prompt, children were able to verbally share the startegies they used. Some very interesting strategies and connections were explored.


Some examples of estimating strategies:

 

 

 

As the sticky notes were scatttered all over the board, a classmate suggested we arrange the numbers in order to make it easier to see how estimates. We agreed this was a good idea and so some of us arranged them in teens, twenties, and thirties/forties.

What is the range of estimates?

- We determined the range was 30.



Why?

- Because the smallest estimate was 12 and the largest was 42.



So, what does the range tell us?

- The difference between the highest and lowest.

- How big of a difference people estimated.


Can we explain what the range is in other ways?

- The range can tell us the middle amounts.


It was then time for the exciting part- counting the sweets to see who would win.

We counted 19 sweets.

No one had estimated exactly 19 sweets, so, who wins?

- Whoever was the closest.

We had two students estimate 20 so they won the sweets.

We wanted to hear again what strategy they used, so those learners shared again the strategy they used when estimating.


When counting the sweets, some wonderings emerged which we have added to our wonder wall:

- Do the companies count out the sweets per jar?

- How do they know how many sweets to put in the jar?

- The jar says it is 45 grams, so do they measure the mass of the sweets?

- Do they just estimate the number of sweets?

- Would all the jars have exactly 19 sweets?


And some theories were discussed:

- The jar was packed full, so maybe they are thinking of the volume of sweets- the maximum amount that fits in.

- Since it says 45 grams, I think they must weigh the sweets but they round them up or down so if the sweets weighed 48 grams they would say that is close enough.




Obviously, the opportunity to win some sweets enticed the children a lot. 

Having regular maths prompts / invitations as part of a morning routine can (even without winning sweets) help engage children in creating or testing mathematical strategies in relaxed and real life context ways.

They can also serve as an interesting informal assessment when spending time listening to or reading strategies each child is trialling to use. Often, they come up with really creative ideas that can be tapped into for further investigations.

Valentine's Ratio Problem

It's St. Valentine's Day.

We began our day writing messages about what we love / appreciate about us as a community of learners. We enjoyed reading this out and discussing the ideas in a circle. 

 

 

 


It's always good to create a positive atmosphere and to constantly guide children to appreciate others. :)





To help feel festive about the day, we looked at the following problem:

I was hoping this would help us inquire into using a ratio table or double number line naturally as we haven't directly looked at these as a visual strategy yet. 

As per usual, we had a choice of trying to solve this visually individually or with a partner. The key word was solving it in a visual way. 

After experimenting and lots of deep dicussions- especially testing whether answers made sense or not, we discussed some of the strategies we were interested in finding out about and those children explained to us.

Here are some of the strategies:

 

We really liked all the different approaches of visualising and we discussed how it didn't matter whether we got the answer or not. Instead we should celebrate the creative thinking that took place. 

Obviously the double number is still a new concept and so I introduced it as a possible tool we could use in future inquiries:

Some of us liked this strategy and others preferred their own as it made more sense to them. Thoughts like that are really as mathematicians. Whatever helps us to make sense of numbers is what we should use another child remarked. And that, was a pretty perfect way to move on to our next investigation. 

Multiplying Decimals

As part of our Unit of Inquiry exploring forces, today we were going to find out how much we would weigh on different planets- the kids love it! 

Part of that requires multiplying their body mass with decimals.

So, to better understand what we will be doing with the numbers, we began with this lead in:

We used the think-pair-share strategy.  Firstly the children jotted down different ways. They then shared with their table group and then we discussed and shared ideas as whole class.  Some of the key understandings included:

We have done this a few times over the year and each time additionally unique perceptions are shared which I find really interesting. I can see how some children's conceptual understandings and abilities to express have expanded and deepened. 


The whole class sharing raised some interesting discussions such as a child sharing how decimal numbers are like negative numbers.  

- Are they? What do we think about that?

Some of us agreed, some disagreed and many were unsure.

Another asked: Can we have negative decimals?

- Can we?

We thought of having a temperature of   - 1 . 5 ° C

Does this prove we can have negative decimals?

Does this mean a decimal is a negative number?

A student shared a theory that: 

This really got us wondering: Can a demoninator be zero?

We chatted about what this might mean- Can we have zero whole parts?  Could this represent a decimal as a negative number?

It was a very interesting thought and I explained that we will definitely come back to this in a few weeks when we explore negative numbers. 

Some of us still weren't 100% sure about decimals being negative numbers or not and that is ok. I think it's good to keep wonderings floating in our minds to think more about later. 



Having tuned our minds back into what a decimal is, we then looked at the following: 

I posed this question to help build number sense and to also value creating theories which we are always doing. 

We showed with thumps up, down or sideways what we our theory was.

There was a mixed initial thought to this.

To help each of us find out for ourselves, the following was posed: 

Asking 'How many different ways......' is a great way to encourage deeper thinking and creativity.

If we ask children to think of one way / one answer, we are limiting their potential to discover different ways of thinking.

Again, we used the think-pair-share routine. 

It was interesting to be able to walk around and chat / observe the different ways the children were trying to visualise it. 

One children shared a great hypothesis:

When we multiply numbers, the answer is bigger so my theory is that the answer to 5 x 0 . 5 will be bigger.

This completely makes sense and I love how she has drawing upon prior conceptual knowledge to create and test a theory.

After a while, the children shared with ther table partners their visual ways. Each table group were asked to select one of the visualisations that they thought the whole class would benefit from seeing. 

Together we discussed the following shared:

We appreciated all the different ways we could visualise the numbers.

We then repeated with a larger decimal:

Again, we first estimated and then tested by visually drawing what it looks like in different ways.

Some of the table sharing included:

We really loved the creative story behind the one below. He explained how there were 5 whole people at the airport and each carried a bag that was 0 . 25 of their body mass:

Valuing creativity and visualising in maths can greatly help children to make stronger number sense like these examples show. 

Lastly, the children created and visually showed their own number sums. Afterwards, they shared and discussed these with their table partners:

Some wanted to challenge themselves further by multiplying a decimal with a decimal to see what it looks like:

And this student found it very interesting to discover how small the number would be when multiplying 5 by 0 . 0000002. We giggled about it being about half the size of a ladybird's poo :P

Before moving on to multiplying the gravitational force of our mass to see how much we would weigh on different planets, I asked if we had some wonderings we wanted to explore next week and so we have the folllowing to find out about: 

I think this has helped us launch into some really interesting wonderings to explore that will further help develop our number sense with decimals and fractions.