I played around with designing a Christmas tree and to my surprise, could create it with an exact area of 100 square cm! (Got to love when maths works out for something you intend):
Without knowing, the children began drawing their Christmas tree until it would create a total area of 100 square cm.
They started sharing some interesting patterns that emerged such as each row increasing by odd numbers.
We wondered why that happened and some shared an understanding that because we start with an odd number (1) and we keep adding 2 to each row, then the rows will always be odd numbers.
We know now in our class that we should always be thinking of the whys in maths, so its great to see us now leading those why questions without me needing to prompt that anymore.
Another student shared an interesting pattern. He saw how the bottom row of 19 added to 20 with the top row of 1. We could continue the pattern:
17 + 3
15 + 5
13 + 7
11 + 9
A student wondered if the add to 20 because a fifth of a 100 is 20. She played around with that theory for a while whilst we continued (She later shared that she couldn't find any real connection, but we appreciated her thinking and the ways she tried to find out)
So, what could we do mathematically with our Christmas tree?
- Someone shared how they could see it is symmetrical so we all found the line of symmetry and added it to our tree.
What else could we do mathematically to our tree?
- We could add 1 square cm baubles to decorate it.
How is that mathematical?
- They are each 1 square cm in area.
We liked that idea so we draw 1 square cm baubles on.
What else could we do mathematically to our tree?
- We could colour them to find their fractions.
So, we coloured in our baubles.
We then created a key and thought of the fraction of each bauble colour compared to the entire area of the tree.
A student reminded us that we should simplify the fractions if possible.
Why should we simplify fractions?
- Because when we simplify them, they are easier to understand.
For example, 1 / 2 is easier to understand than 32 / 64
- If you were ordering a pizza, it's easier to visualise a third of a pizza rather than trying to understand 6 /18s.
What else could we do mathematically to our tree?
- We can convert the fractions to decimals or percentages. It will be easy to do since our tree is 100.
What else could we do mathematically to our tree?
- We could find the fraction of each bauble colour to the total number of baubles.
So, we did that too.
What else could we do mathematically to our tree?
- We can find the area of the tree that isn't decorated by baubles.
So we did that too.
So, what do we think about this?
- Wow! We can do so many mathematical things with just a shape!
- This helped me see what percentages look like.
- I liked how we needed to think of how to see it mathematically.
- I think tomorrow, we should create a star for the tree and then we could measure the angles in it.
We loved that idea so will do that tomorrow.
I think it will be interesting to see what we come up with to create our mathematical menorah lamps tomorrow:

Mathematical Hanukkah Menorah Lamps:
The next day we did a similar activity. Some of the Jewish children in our class explained to us how they celebrate Hanukkah and the meaning of the menorah lamp.
We then decided to be able to investigate percentages easily, we should try to create a lamp with an area of either 100 or 200 square cm.
After creating them, we then coloured them and calculated the fraction, % and decimal amount of each colour on our lamps.
Some samples:
Area of 100 square cm:
Area of 200 square cm:

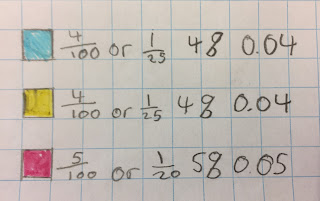
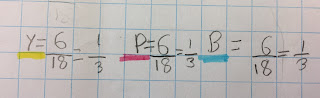




I love that "So, what could we do mathematically with our Christmas tree?" Graeme! There's a bit of an empty space there. It throws the classroom - teacher and students - back on the questions they decide to pursue. And you came up with some great directions!
ReplyDeleteHi Simon, Hope you enjoyed the holidays too :) Thanks for your feedback- sometimes taking risks can really pay off. It could have been a 'tumbleweed' moment, but happily far from it.:)
Delete