Inquiring into the Square Metre

Inquiring into the Square Metre


There is a common misconception that a square metre has to be square in shaped.

When children are introduced to square centimetres and square metres, its easy to understand how this misconception grows.I wonder though if it prevents children from being able to deepen their conceptual understanding of surface area.

I wonder if by constantly having children use square cm and square m as a unit of measurement, are we denying them from really understanding how surface area is a measurement of space rather than a measurement of number of square cm etc.


To help address this misconception and to deepen our conceptual, understanding of surface area, the children entered and saw a piece of paper on the floor surrounding by metre rulers:

We did a 'silent gallery observation' where children came up close and observed what they saw and then returned to their see-think-wonder paper to record their thinking. They could keep returning to the display as much as they wanted:

After recording, the children shared their ideas with their table partners and then we shared and discussed some of these as a class:

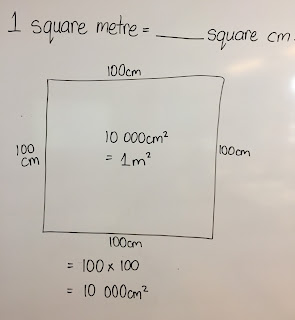
We thought the first wondering was interesting, so in pairs we found ways to try to find out how many square cm equals 1 square metre.

We had quite a few different ideas and strategies.

When students shared, one in particular stood out where she showed how we measure the area of a rectangle:

She then used this explanation to explain how we can find out using the same strategy:

We thought 10 000 was a lot, but also interestingly, when we sat around the square metre paper again, a few of those commented that it seemed there were a lot more than 10 000 fitting inside it.  I had to agree.

I then posed the question: Does a square metre have to be square in shape?

We wrote our theories on a post it and then posted them on the line (above).

We noticed how it was almost 50-50.

We heard from some people who thought it had to be a square and their reasonings.

We then heard from others who were in the middle and finally we heard from those who thought it doesn't have to be square in shape.

To help with the debate that took place, I then cut part of the square metre paper.

I then moved that cut part and joined it to another part of the paper.

What shape have I created?

- A decagon.

Is this area still 1 square metre?

We had a stand off again with a 50-50 opinion.

We heard some ideas and their reasonings.

One student then remarked how it is still 10 000 square centimetres and that's why it is still 1 square metre.

Ohhhhhhh.........

Light bulbs started flashing all around.

Another then remarked,so if think whether the surface area is 10 000 square cm, then we will know if it is a square metre.

We all agreed.

Estimating is a key skill we should always encourage children to do in maths. When we estimate numbers etc, we are gaining a deeper sense of the concept.

We then did a hunt for objects in our room that we estimated had an area less than, approximately equal to, and greater than a square metre.

After gaining a better sense of the size of a square metre, we then thought about how we could create different shapes that had a surface area of 1 square metre.

Children partnered up with others and sketched possible ideas.  Loads of rich reasoning discussions and creative ideas took place.

Some samples:

We partners felt confident in their measurements, they then used masking tape to create their 1 square metre shapes.  We didn't have time to finish these, but when we do, we will then examine the shapes created and see if they are or are not square metre in area.

This pair had sketched a square metre and then split it in half. The then joined the two triangles and worked out the lengths:

Some amazingly creative shapes are been explored and we are all excited about making and sharing them tomorrow......

Polygons with the Same Area, but Different Shape

Returning back to one of our student questions placed on our maths wonder wall:  "Is the area and the perimeter answer the same?"  we chose a number and then creatively drew as many shapes as we could that had the same area. 

Rather than doing this in one sitting, we spent about 5 to 10 minutes every few days revisiting this to create more shapes.  This strategy hopefully helped to reinforce the key understandings they were discovering themselves about mathematical space, area and perimeter whilst also keeping engagement high rather than a doing this as a solid 20 or 30 minutes.  The children experimented with drawing their polygons in the maths books and today published those they were the most proud of creating (samples below).

Children chose numbers such as 7, 12, 16 22 etc.....



All of these polygons drawn have an area of 7 square centimetres:

Lots of natural questions arose such as the names of different-sided polygons which the students found out on the net.

It sparked a lot of creative thinking as well as developing reasoning and problem-solving skills.......

Some sample reflections: What did this learning experience help me to understand?

- I learnt that polygons can have different shapes and perimeters,but the same surface area!

- When finding the name of a polygon, the size doesn't matter. What matters is the number of sides it has.

- I learnt that there is a pattern in the naming of polygons. Eg, if you want to know what a 16-sided shape is you just add 'hexa' + 'decagon.

- I learnt that there are interesting connections between polygons; this activity helped me deepen my understanding of angles too.

- It helped me to understand that no matter what the area of the shape or if the shape is irregular, it can still have the same amount of sides.

- It helped me understand that a square centimetre or a square metre can be a different shape other than a square.

Perimeter Ratio Maps of Home Countries

Is a country's border the same as its perimeter?

It was a good question asked by a student today and we used it for the basis of the following problem-solving activity.

The children selected a country that connected with, found the border length on the net and then needed to create a ratio key of what 1 cm would equal for their map.

Sounds simple, but actually a lot of perseverance and thinking was needed in firstly an appropriate ratio and secondly how to draw it using the cm grid lines so that it would shape roughly like the country and match the number of cm needed.  


Here are some samples of some students who have already completed their maps:

(This student got mixed up with the ratio as it ought to read:  1cm = 28km)

Real Life Maths: Measuring the Area and Perimeter of Our Homes

It's important for children to gain deep understandings of how we use the maths we explore in our classrooms to real life situations.  If children don't understand the relevance, their engagement and curiosity diminishes. 


To help us find out how we measure area and perimeter in real life, we began by measuring them on this fictional house floor plan. 

We discussed the ratio key and techniques used in the drawing as an example:

For home learning, we then created floor plans of our own flats/houses and measured the area and perimeter of each room:

When sharing our floor plans in groups, we asked each other the following questions as an oral reflection:

° What strategies did you use to measure the area and perimeters?

° What challenges did you face and how did you overcome them?

° What did this activity help you to understand about area or perimeter?

As a whole class, we discussed how much we enjoyed this maths activity and a few remarked how it also helped deepen their understanding of how we use decimals in real life too. 

Real life maths always engages and provides deepened understandings for children than a dreary worksheet or textbook could ever hope to achieve......

Creating strategies to measure the area of shapes

One of our wonderings we displayed on our wonder wall was how can we measure the area of other shapes other than rectangles which we already knew how to do.  

It was a great question and so today we started exploring it.


We reviewed together what we had discovered about finding the area of a rectangle and a triangle. 

I then drew this type of trapezium on the board and the children had some time trying to figure out how we could measure its area.  After hearing quite a few 'wow' moments flashing in the room, a student shared with us the strategy we can use: 

Giving them a paper with images of regular and irregular polygons, types of quadrilaterals and types of triangles, they chose shapes and tried to create ways we could measure their area.

Some really creative ideas started emerging. They weren't necessarily the easiest way to measure the area, but in mathematical thinking creativity is important so we didn't dispel their strategies when we shared what we had discovered. 

This student started discovering how we can find triangles inside regular polygons:

This student came up with a really creative way to measure the area of a regular octagon:

Here is another creative discovery made.  We can split a decagon into a rectangle, 2 trapeziums and 2 triangles. Amazing!

Here a student discovered a way to measure the area of a kite, a parallelogram and a different way to measure the area of a square. She knew the easier way to measure the area of a square was to simply multiply its length and height, but wanted to challenge herself to see if there were other strategies:

We will continue exploring such strategies over the next few days.

All of this amazing mathematical thinking stemmed from a student wondering how can we find the area of a hexagon.  When we value student questions, this is the type of authentic enquiries and mathematical thinking that can take place in our classrooms. This became an engaging and rewarding problem solving and mathematical reasoning learning experience which also created a lot of self-pride in the students when they started making their discoveries.

Students create our area / perimeter planner

We were introduced to our central idea today and brainstormed things we were curious about and felt would help us to have a deepened understanding of our central idea.  This is what we have decided our maths unit should entail:

Creating big guiding questions like these in the beginning of the unit make the learning student-owned so the kids are instantly more engaged. Another great benefit to this is it gives the students a framework to make their own enquiries to discover and share with their peers. 

Having this displayed in our room, we will continue to refer to it and think of things we could do to find answers to our questions.

Area & Perimeter Intro

We began our new unit today exploring the central idea:

We can use different strategies to more easily measure the area of surface space or the length of perimeters in our daily lives.

Sometimes we begin out new maths units by unpacking the central idea, but for this unit we began with a provocation.

Firstly though, on the board I wrote:

Perimeter is.........

Individually, the children write down their own definition to explain what they remember it to be.  They then shared their definitions with their table partners and we then shared together as a whole class.

Key words we felt we needed in our definition were: measurement, outside of shapes and length.   We felt that provided we had those, our definition would be solid.    

We repeated this with:  Area is.......

Whilst sharing as a class, we were able to disspell some myths some of of us had about what area is. In particular, some of us hadn't thought about area being surface space and their definitions could apply to volume as well as area. This aroused interesting discussions of how the volume of space is actually quite different to surface area and we came up with some examples of both.

We discussed how perimeter and area can be confusing at times and what their connection with each other is like.   We are still wanting to create a memory hook for each to help us not get confused and so will look back at this later in our unit.

With these understandings, we began with this question:

Children drew different sized 'paddocks' and calculated their areas and perimeters.  Some came and shared what they did and then a great question was raised:

But, can the area and perimeter sometimes be the same number?

We wondered about that and so experimented with different types of shapes and their sizes.

We found that a square with sides of 4 does actually both equal 16.

Someone then made an interesting theory- perhaps any regular polygon with the same sides might also equal the same.  

We thought about this with the example a student suggested:

- an equilateral triangle all with sides of 3.

But then, we realised we don't know how to measure the area of a triangle so we put that question on our maths wonder wall:  How do we measure the area of a triangle?

This sparked more curiosity. what about the area of a hexagon or an octagon? 


This is the exciting part of inquiry-based maths.  When those genuine questions start popping up and which we will explore in our unit.  

As we are battling with rain this week, we left those great questions for tomorrow and instead used the dry patch to explore area and perimeter outside. 

_______________________________________________________________

We then discussed the following two provocation questions.  Students had a choice of which they wanted to try to solve and whether they wanted to do them individually or in a small group.

The I.S.L Board has decided it is time to replace the astro-turf on the football pitch as it is getting old and the children keep slipping over on it.

The cost of the astro-turf is CHF 8.50 per square metre.   So, they have decided they will use that for the football pitch itself, but the surrounding area will be surfaced with a cheaper astro-turf at CHF 2.25 per square metre.

Additionally, the lines on the pitch require repainting. The special, adhesive paint costs CHF2.50 per metre. Find an EASY strategy to calculate the cost of repainting the lines on the pitch.

They have asked you to calculate how much it will cost to resurface the entire football pitch area.

It is time to repaint the tennis court areas. The I.S.L Board has decided to repaint the tennis court themselves with a special non-slip paint that costs CHF 4.75 per square metre.  

Surrounding the tennis courts, they will use a cheaper paint which costs CHF 0.75 per square metre.

Additionally, the lines on the courts require repainting. The special, adhesive paint costs CHF2.50 per metre. Find an EASY strategy to calculate the cost of repainting the lines on the all the pitches.

They have asked you to calculate how much it will cost to repaint the entire tennis court area.

Every student was completely engaged and excited about trying to solve these questions.  Hands on maths usually does have that great effect!

Afterwards, I saw this great quote on Twitter via #RMEWillows.   Hoping this intro lives up towards at least some of it: