Today, we began by looking at the definition of 'prime':
We identified the definitions that best related to prime numbers:
We then recalled how the word 'composite' comes from the base word 'compose' and how the definitions of these words can help deepen our understandings of what prime and composite numbers are.
It helped remind us of yesterday's investigation into how prime numbers are the 'atoms' of whole numbers.
We then spent time collecting our thoughts and reflecting on what we have already discovered about prime and composite numbers for about 5 minutes using a Venn diagram.
After we reflected, we then shared our understandings with our table partners.
This, I feel is a useful strategy to occasionally use to tune in to what we will be exploring that day.
Creating a Venn diagram also helps arouse children's curiosity of what things they might discover to add to later and by having children discuss and share, theories and learning grows.
We then reviewed what we had learnt about atoms and the analogy we are using between atoms and prime numbers.
We remembered that just like atoms make up all matter, prime numbers when multiplied can make all numbers.
This spiralled into connections and discussions about scientists trying to split the atom in CERN, the Big Bang theory and how mathematics is a tool for trying to understand everything in our universe. Such is the nature of an enquiry-based classroom :)
We were to continue trying to make numbers by finding the factors of primes. To make it a bit interesting, we looked at a YouTube that shows a computer programme finding all the prime numbers between o and 9 999 999 (there was a strong interest yesterday looking at the world's largest known prime number).
The YouTube is almost 14 minutes long so we used that as our timer.
We were fascinated watching the prime numbers appear:
Let's see what number we can reach within that time frame.
Loads of wonderful testing and thinking took place:
We shared what each number each partner had reached and we helped each other out with numbers we had find tricky.
32 was only of them, so solved it together.
64 was also tricky till somehow saw the connection that 64 is half of 32!
Looking at our 'atom' numbers, we readdressed one of our big wonderings:
To help scaffold our thinking, we began by theorising:
Can 1 be a composite number?
We used our 'atom' creations and our previous definitions of a prime and composite to help us.
Partners discussed and wrote their theories down.
We then shared our thoughts:
We liked the idea shared how 1 is like an atom- its indivisible, but it is breakable as we can break it down into decimals /fractions.
I know that prime and composite numbers need to be positive, not negative. But I didn't want to 'kill' this wondering. It's a great question for us to enquire into later. As we have recently enquired into positive and negative numbers, thsi could be a great investigation soon.
Most of us concluded that 1 cannot be a composite.
So, can it be a prime number?
To find out, we looked at our 'atoms' again and this time tried to find a different way to define what a prime and a composite number is using factors.
Partners discussed and wrote their ideas down before sharing.
In sharing, we were able to add the following to our definitions:
( We deleted 'has to be add-except for 2' because a student suggested its 'too messy' for a maths definition, and we agreed)
Now we were ready to look at 1 again.
So, most of us have concluded that 1 is not a composite.
So, what is it?
Partners discussed, wrote their theories and shared.
Most of us concluded that based on our definitions, 1 is neither a composite nor a prime number.
I explained how I happened to know that 1 originally was considered a prime number, but later it was removed.
Why?
We looked at our 'atoms' again for possible clues.
Eventually a pair shared their theory:
If 1 is a prime number then our definition regarding factors needs to change and becomes 'crazy'.
How so?
They explained using the number 15:
If 1 is considered a prime, then every number has an infinite number of factors.
So what what the definitions of a prime and composite look like?
Together, we created these definitions:
Looking at these, we could easily see how 'crazy' the definitions would be.
So, we figured that must be why 1 is no longer considered to be a prime number.
Another student used this to show her understanding using our atom analogy:
If 1 is a prime, then the number 15 would have an infinite number of atoms making it. She remembered what we had learnt about water being H20 and concluded that the number 15 would change each time we added another 1 'atom' to it.
So, 1 isn't prime nor composite.
What is it then?
- It's a special number.
- It's the first number that all numbers come from.
- It's the first unit in the units place value column.
With that last thought, I shared how some mathematicians do actually call 1 a 'unit'.
When we think of the word 'unity' we can see how the number 1 unites all numbers. That's what makes it special. Too special perhaps to be called a prime or composite.
This then raised the question: what about zero?
I love it whenever we think about zero and so do the children.
We reflected on what we had already discussed about zero over the year.
Can 1 come from nothing?
This is one of the biggest questions that mathematicians, scientists, theologians and philosophers have been trying to answer for ages.
Anyone who is able to define what zero is and how 1 can come from nothing would win a Nobel Peace Prize and instantly be world famous.
If we can find evidence of how 1 comes from zero, we have discovered how and why everything in the universe was created and perhaps what its future holds.
- Like the Big Bang Theory?
Exactly
The singularity of the Big Bang is like the number 1. Everything in the universe came from it just like all numbers come from 1.
We can have 1 stick and break in half.
What number have we got?
- 2
What have we created if we break the 1 stick into thirds?
- We've made 3.
and so on.
We can prove that all numbers exist because of 1.
But how can we explain where 1 comes from?
How can 1 come from zero?
A student shared: So maths can tell us everything about the universe?
- We thought so.
We had almost run out of time.
It's important to reflect, so we added new understandings or theories to our Venn diagrams we had begun with:
In addition to being a really important learning strategy, reading through them helps see any misconceptions that might be popping that with some children to be addressed later in our unit.













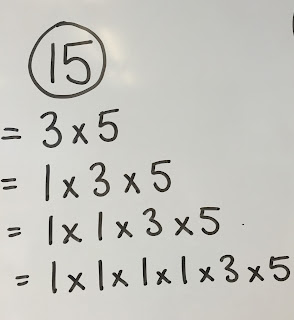




No comments:
Post a Comment
What do you think? ...........