After our initial exploration of prime numbers yesterday, we began by thinking about why prime numbers fascinate people.
Essentially- Why are we enquiring into them?
We briefly recapped what we had learnt about the Ancient Greek mathematician 's strategies for identifying the prime numbers in a hundred grid. (We had started this ourselves yesterday)
We drew a timeline and noted how Ancient Greece was between 800 and 500 BC / BCE.
We know that prime numbers have been fascinating people for at least 2 500 years. But why?
One student remarked that maybe even the Ancient Egyptians explored them before the Greeks. We thought that was plausible.
What about today?
How do prime numbers continue to fascinate people today?
To find out one reason, we watched this fabulous YouTube explaining the discovery of the recently found largest known prime number.
We paused occasionally and discussed.
It IS incredible!
A lot of wonderings and theories were shared in our discussion.
800 computers working together- that is definitely a LARGE calculator!
We had also paused to look at the largest known prime to really try to understand what it is:
This proved useful to help correct some misconceptions some of us had about the meaning of 'to the power of'.
To help we shared our understandings of what 'to the power of' means:
We thought trying to comprehend:
was really mind-bobbling!!!
And we thought it fascinating that a number so large is calculated and then we need to subtract 1 to make it prime. Why subtract 1?!?
Could it have something to do with one of our wonderings a student asked us:
Some of us felt there might be connection.
Other students wondered if we we changed the 2 to another digit like 4 and kept the same 'to the power of' and subtract 1, would that also be a prime number?
Just wonderful theories like this are brilliant!
We were wow-ed by the fact that this newest discovery was larger than the previously known largest prime by 5 MILLION DIGITS!!!!
It's a definite WOW factor for both the children and myself to try to wrap our heads around!
But why find these large prime numbers?
Some of us have begun our home learning choice researches and were able to share how computers use prime numbers especially banks for online purchases. Our credit cards are given large prime numbers to access the bank's money. The prime number is like a key to the lock.
Militaries also are willing to pay millions for new prime number discoveries for coding and encryption!
Others shared how they could see some people loving the challenge of finding the next largest- even being a personal passion another added.
Looking back at our timeline we thought again: Why have prime numbers fascinated people for such a long time?
We had certainly added to our previous understandings.
To help us further, I wanted us to discover how every positive, whole number is made up of the factors of primes.
I wanted the children to make this discovery for themselves.
So, we brainstormed what we knew about atoms.
We then watched a part of a YouTube explaining What are Atoms? (for kids)
We discussed what we knew about the atoms of water.
H2O meaning two hydrogen and 1 oxygen atoms.
Using this as an analogy, I presented this question for partners to try to solve:
We looked at our list of prime numbers we had already discovered and the composites.
As partners explored possibilities, we reminded ourselves that like scientists we should be creating a hypothesis and testing them out.
After about 5-10 minutes we shared some of our hypotheses we were creating and testing- both successful or 'un'sucessful
Some had thought of trying to make composite numbers by adding prime numbers. The prime numbers being the 'atoms'.
They were finding this worked for some numbers but not others.
Others shared how they were trying to divide and others subtract.
Others were experimenting with multiplying:
They weren't certain yet, but it seemed so far from their testing that we can make composite numbers by multiplying primes.
Another group added that they were testing that maybe you only needed 1 prime number such as with 42.
After this initial sharing we spent some more time experimenting with the numbers either continuing with our own hypotheses or trying to test out others shared.
We then had an 'Eureka!' moment!
One pair excitedly shared how they had proven their hypotheses!
They strongly felt that we can make every number out of primes. Either the number is a prime itself and therefore exists alone (like an atom) or we can multiply the factors of primes to make all other numbers!
We looked at this together:
1 - Hmmmmm...... we still don't know what it is. Maybe its prime.....
2- is a prime so exists as an 'atom'
3 - ditto
4 - made of the factors 2 and 2 (prime)
5 - a prime
6 - 2 x 3 (both primes)
7 - prime
8 - 2 x 2 x 2
or 8 to the power of 3
9 - 3 x 3 (prime)
10 - 2 x 5 (both prime)
11 - prime
12 - 2 x 3 x 2
This excited us!
Could we REALLY make every whole number by factoring primes?
To help with our analogy of 'atoms' that would hopefully help us to understand why primes are so fascinating, we used this hypothesis and created each number starting at 1 and made the numbers look like atoms joined together with prime numbers.
Some great head scratching took place.
Samples of making numbers using the 'atoms' of primes:
Trying to make 32 our of factoring primes remained a challenge for a few partners by the time we needed to finish up for the day.
We will continue this investigation tomorrow to help solidify this understanding of why prime numbers fascinate mathematicians.
To reflect, sometimes I use the strategy as a whole class of '5 things'.
So, what are 5 things we have discovered about prime and composite numbers today?
- They might be the atoms of all numbers.
- People can become rich or famous by finding new ones.
- Composite numbers can be made by factoring primes.
We paused there.
Let's look at the word 'composite'.
what word do we see inside it?
- compose
What does compose mean?
- to make
- to produce
So, why do we think they are called composite numbers?
hmmmm.......
- Oh! Because those numbers are composed of primes! They are made of prime numbers!
What do we think? Is that plausible?
We agreed to seemed so.
Two more things we have discovered today?
- 1 plays an important role in finding large prime numbers. For some reason subtracting 1 helps.
- Like scientists finding out what is inside matter, as mathematicians we can find what is inside a number.
- Could prime numbers be like the primary colours? Remember how we learnt that all colours are made of primary colours? Well, maybe prime numbers are like them?
Sometimes, we can't script such perfect ways to end a learning session before heading out to lunch and us agreeing we should enquire into that interesting idea tomorrow.
I loved that closing thought. :)






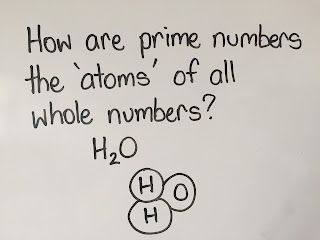






No comments:
Post a Comment
What do you think? ...........