What I thought would be a pretty basic learning experience of trying to find the largest prime number turned into an extremely engaging and higher order thinking experience.
As we are coming to a close of our unit exploring prime and composite numbers, I looked at our wonder wall wonderings and thought we could explore our question:
How can we find large prime numbers?
It's great question and since we have already explored the largest known prime to date, I know our interest in this is high.
So this was what was proposed for our investigation:
What do we think about this 'win-lose' ranking?
- Those who find the largest, 2nd, 3rd, 5th, and 7th largest prime numbers will 'win'.
- Only those who find the 4th, 6th, 8th or 9th will be have 'lost'.
Exactly.
We thought this added some extra spice to the investigation.
Admittedly, I wasn't really sure how this was going to pan out. I figured most would try to find prime numbers between 100 and 200, a few might try for a number in the thousands.
What happened though, blew me away.
We really did gain a real sense of how challenging it is for mathematicians to find unknown prime numbers!
Some of us also experienced the pure elation when they discovered a prime as the shrieks and cries of excited joy testified.
After the time was up, we shared our largest prime numbers we could find:




Being 10 / 11 year olds, you might also think this are random numbers they have suggested in hope they are actually prime.
Having each pair explain the strategies they tested and how they came to these numbers as possibly being prime numbers was incredible!
Amazing mathematical reasoning and experimentation took place.
I was floored!
We then experimented with ways to try to determine whether they really were prime or composite.
Googling didn't offer much help with the really large numbers.
Testing those large numbers with our own strategies did start to eliminate some numbers as being composite.
We thought this idea for determining a prime was really interesting:
They reasoned that if they changed that largest prime to be a 6 to the power of and subtracted 3 instead of 1 it might make it a prime number.
Thinking about this, someone reasoned that it might be composite because:
We really appreciated the logical thought behind it though and still wonder whether it is or isn't a prime.
I suggested we ask the head of maths in secondary to come take a look at it and see his thoughts, so we'll wait to see his thoughts too.
This pair found 2 prime numbers!!
131 071 is a prime. It is small enough for us to google it.
We were really curious about their other MEGA number and were blown away by it:
They remembered from watch a chosen YouTube home learning last week about monster prime numbers that a formula exists.
2 (powered by a prime number) subtract 1 is a formula for identifying prime numbers. (It's amazing what children remember!)
So, they just multiplied 2 97 times. Literally. On their calculator they typed in 2 x 2 x 2 x 2 x 2 x 2 ...........97 times and that was the number they got!
How amazing is that?!?!
A 10 year old!!
We then reasoned that if we had 2 to the power of their number and subtracted it by 1, then it would identify an even larger prime number and so on.
WOW!!
We had also come across MEGA numbers on our calculators and wanted to find out what the 'e' meant so we googled it and tried to make sense of the meaning:
Some us found out our prime numbers were actually composites when others had tested them out. This testing required a lot of reasoning skills and applying different strategies:
We are still on the fence for that prime number beginning with 6.
In our oral reflections we felt we really gained a deep appreciation for how tricky it is to identify prime numbers, but we also appreciated how we can use strategies to try to find them like some of these tested:
Thinking about all this amazing mathematical thinking that took place really reminds me that when we underestimate children and set the bar low, that's what children will learn.
But when we set unlimited bars, this is the sort of incredible thinking that we can allow children to explore!






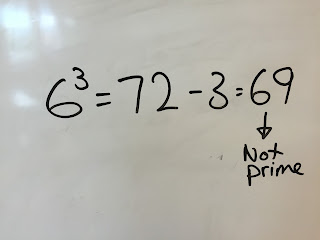



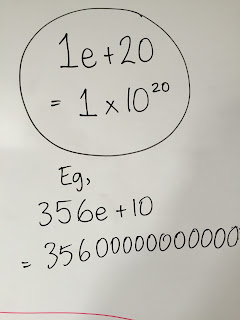


rxtjqnxs
ReplyDeleteglucotrust official website
viagra sipariş
cialis 5 mg al
sight care
cialis 20 mg sipariş
https://shop.blognokta.com/urunler/ereksiyon-haplari/kamagra-100-mg-oral-jel-7-sase-etkili-sertlestirme-ilaci/
cialis eczane